[백준] 1006번 제곱ㄴㄴ수

https://www.acmicpc.net/problem/1016

1016번: 제곱 ㄴㄴ 수

1. 문제 접근

  문제에서 설명하는 제곱ㄴㄴ수를 구하는 과정은 소수를 구하는 과정과 원리가 같으므로 소수를 구할때 흔히 사용하는 '에라토스테네스의 체'를 생각해볼수 있다. 하지만 처음부터 제곱ㄴㄴ수가 아닌 수를 제거해 나간다면 시간초과가 나올것이다. 왜냐하면 첫번째 제곱수4(=2²)의 배수만을 제거하는데도 max가 최댓값이면 (1,000,001,000,000/4)번을 제거해야하기 때문이다. 따라서 '에라토스테네스의 체'와 달리 중복제거가 발생할 수 있겠지만, 문제에서 주어진 범위(min~max) 내에서만 제곱ㄴㄴ수를 제거하는 방향으로 가야한다.

 

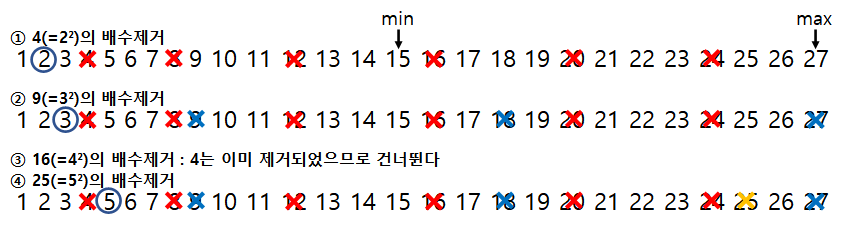
에라토스테네스의 체 처음부터 적용

[그림1]의 ③과 같이 중복제거가 발생하지 않아 효율적이나 min보다 작은 범위에서도 제거가 이뤄져야하기에 시간초과가 발생한다.

[그림1] 에라토스테네스의 체 처음부터 적용

 

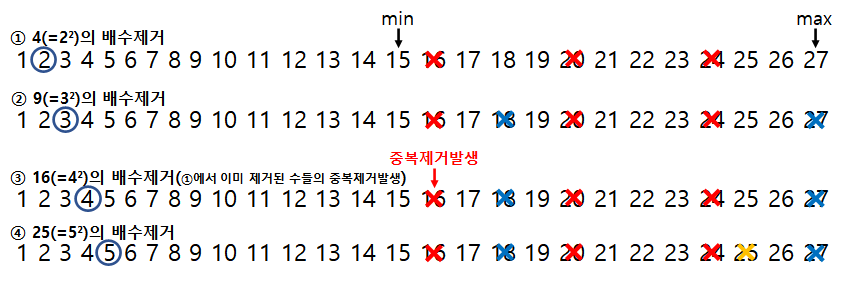
에라토스테네스의 체 범위내에서만 적용

[그림2]의 ③과 같이 중복제거가 발생하므로 비효율적인 부분이 있지만 주어진 범위(최대 1,000,000개)내에서만 제거하므로 시간안에 답을 구할 수 있다.

[그림2] 에라토스테네스의 체 범위내에서만 적용

 

시간복잡도 계산

  가장 시간이 오래걸리는 범위가 min=1,000,000,000,000 ~ max=1,000,001,000,000 이므로 이 범위일때, 시간복잡도를 계산해 보면 아래와 같다.

4(=2²)의 배수제거를 위한 시간복잡도 ≒ O(1,000,000/4)

9(=3²)의 배수제거를 위한 시간복잡도 ≒ O(1,000,000/9)

16(=4²)의 배수제거를 위한 시간복잡도 ≒ O(1,000,000/16)

25(=5²)의 배수제거를 위한 시간복잡도 ≒ O(1,000,000/25)

...

1,000,000(=1,000²)의 배수제거를 위한 시간복잡도 ≒ O(1,000,000/1,000,000) = O(1)

...

1,000,000,000,000(=1,000,000²)의 배수제거 ≒ O(1)

\begin{align} &∴시간복잡도 = O(1,000,000\sum_{n=2}^{1000} 1/n^2 + (1,000,000 - 1,000))\ \ \ \ \ \ \ \ \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ < O(1,000,000(0.64) + (1,000,000 - 1,000))\ (∵\sum_{n=2}^{∞} 1/n^2 = {π^2}/6 - 1 ≒ 0.64)\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ < O(1,639,000) \end{align} 

 

 

 

2. 코드

#include<iostream>
using namespace std;

#define MAX_LENGTH 1000001
#define SQUARED(x) ((x)*(x))

void boolArrInit(bool* jnn, int length) {
    for (int i = 0; i < length; i++)
        jnn[i] = true;
}

int main() {
    long long min, max;
    cin >> min >> max;

    int numCount = max - min + 1;
    bool* jnn = new bool[MAX_LENGTH];
    boolArrInit(jnn, numCount);

    int noJnnCount = 0;
    for (long long n = 2; SQUARED(n) <= max; n++) {
        long long squaredN = SQUARED(n);
        // 아래줄 추가하면 4의배수에 대한 중복제거는 발생하지 않으므로 조금 더 빨라진다.
        // if (n != 2 && squaredN % 4 == 0) continue;
        long long noJnn = (min / squaredN) * squaredN;
        if (noJnn < min) noJnn += squaredN;
        while (noJnn <= max) {
            if (jnn[noJnn - min] == true) {
                jnn[noJnn - min] = false;
                noJnnCount++;
            }
            noJnn += squaredN;
        }
    }

    cout << numCount - noJnnCount << endl;

    delete[] jnn;
    return 0;
}